書誌情報
ICLR2021のオーラル(7,7,7)
論文タイトル:Free Lunch for Few-shot Learning: Distribution Calibration
論文のリンク:https://openreview.net/forum?id=JWOiYxMG92s
この論文を端的に言うと
- 特徴空間で十分な量の訓練データの分布をもとに、新規クラスのデータ分布を推定する
- 推定されたデータ分布からサンプリングし、ロジスティック回帰するとめっちゃ精度でた
few-shot learningの問題設定
簡単には、少ない枚数のデータを使って訓練し、分類タスクなどを解く
例えば、各クラス1枚の画像の訓練データだけを使ってテスト時に5種類のどのクラスに属しているかをあてる → 無理ゲー

一方で人間は右の画像をそれぞれABCと名付けたとき、テスト画像がABCのどれかわかると思う。これは、ABCの他の例を知っているからではない。ABC以外の種類の動物をいくつも知っていて、それらがどういった特徴をもっていると同じクラスであるのかを知っているから
なので、人間と条件をそろえると(?)、他の種類のクラスのデータは大量につかって良い、ということになる
まとめると、訓練データには2種類ある
- ベースクラスとよばれる大量の画像データ
- ノベルクラスからサンプルされる少数の画像データ(N-way K-shot)
※ ベースクラスとノベルクラスはかぶりがない
どうやってテストする? → ノベルクラスからサンプルされたデータがN種類のどのクラスであるのかを予測し検証する

じゃあ、ベースクラスで学習したモデルをノベルクラスのデータを使ってfine-tuningすればいいのでは!

ナイーブにはそうで、普通に精度けっこうでます
関連研究
fine-tuning系
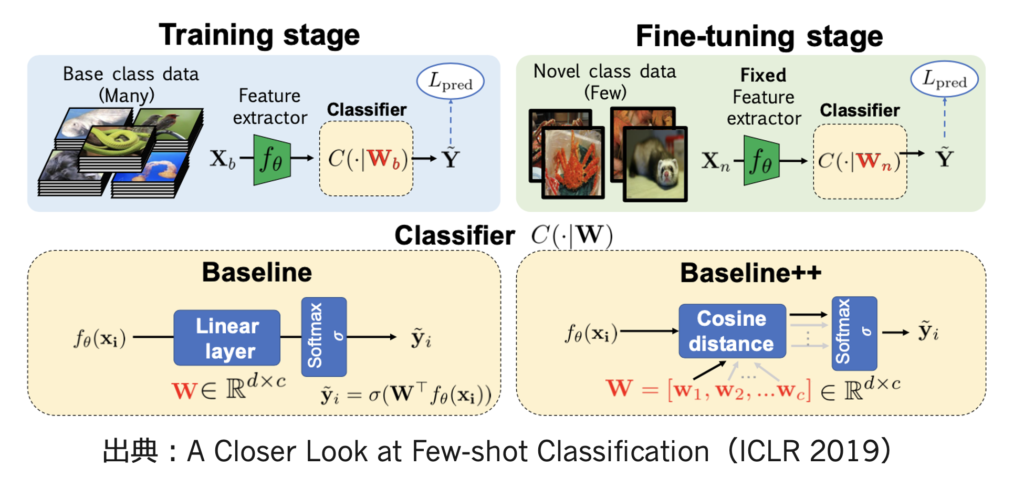
- まず、普通にベースクラスのデータを使って分類器を学習
- その後、最終層の重みだけをノベルクラス用に学習する(Baseline)
- 実はこれだけだと対して精度でないが、内積ではなくコサイン距離を使うとけっこう精度でる(Baseline++)
メタラーニング系
一方で、few-shot learningといえば、メタラーニングというイメージの人もいるのではなかろうか
- ベースクラスからサポートセット・クエリセットと呼ばれる少数のサンプルを何度もとりだして、学習の仕方を学習する
- 具体的な例としてProtoNet(NIPS 2017)を考える
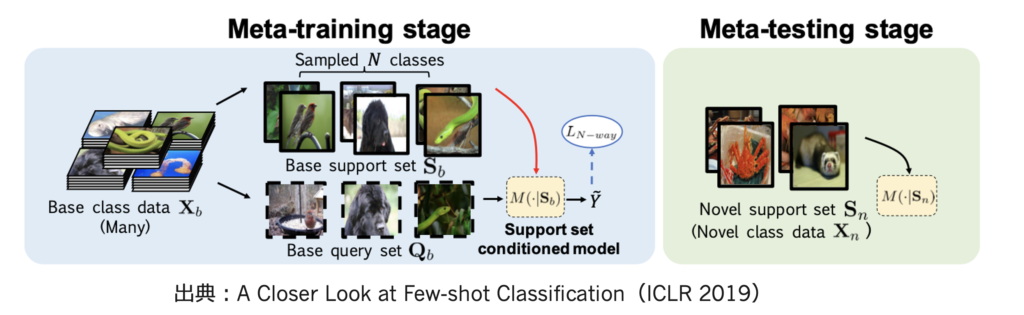
Prototypical Networks for Few-shot Learning
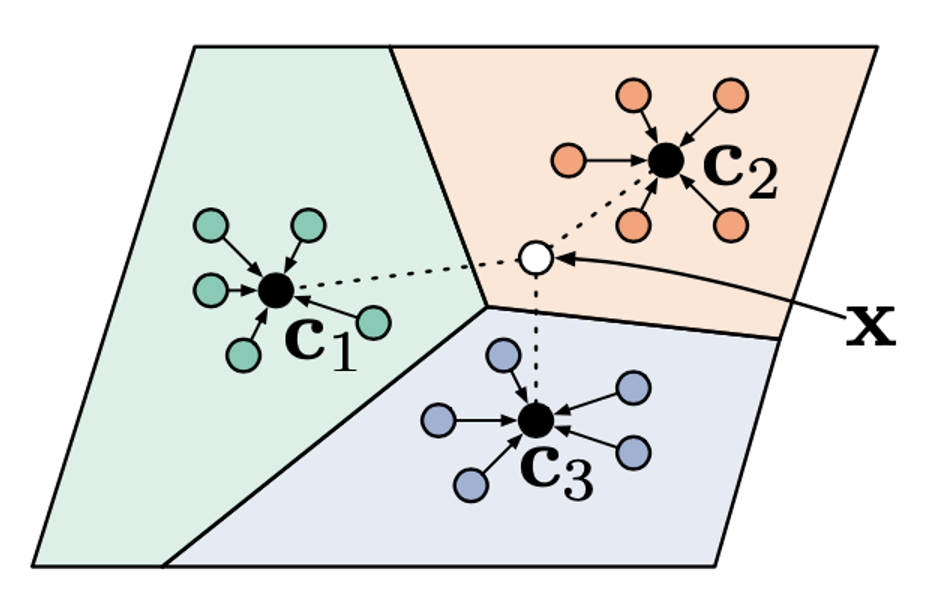
例えば3-way 5-shotのサポートセット(S)をベースクラスからサンプルし、特徴空間の中心点を求める
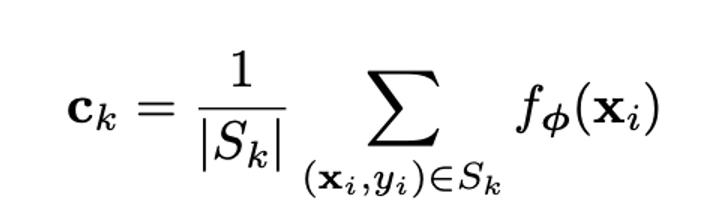
なんらかの距離関数を使い、新しいデータ(クエリセット)と中心点の距離をもとめ、ソフトマックスでクラスを予測し、学習する
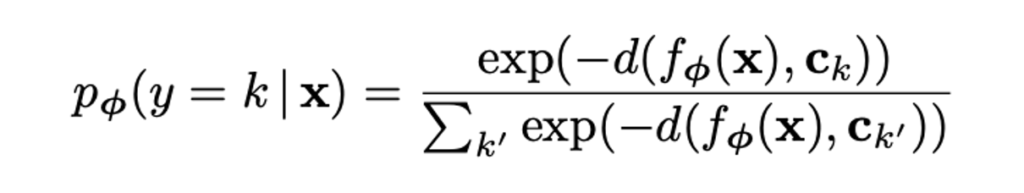
上記を何度も繰り返すことで、少数データからクラスを予測するすべを学ぶ(メタラーニング)
ProtoNet以外にもいろいろメタラーニングのアルゴリズムはあるが、結果を見る感じ、結局ファインチューニングでええやん?といわれている(出典は下)
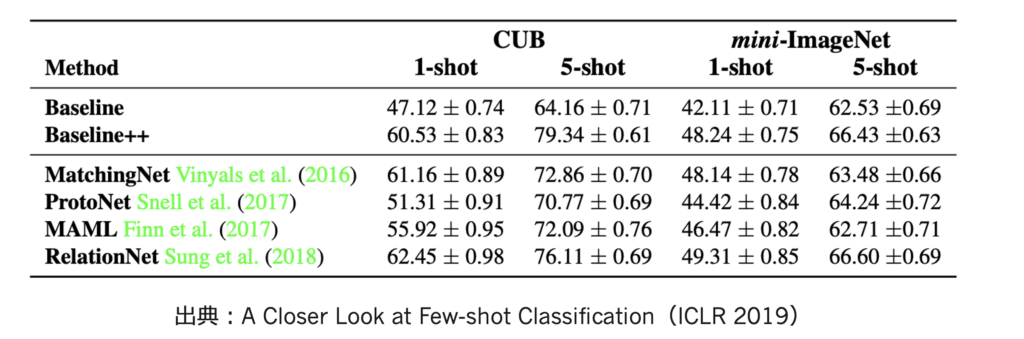
提案手法

最近の流れがわかったということで、今回紹介する論文の内容に入っていこう
提案手法の仮説
まず、ベースクラスをもとに学習された特徴空間上のクラスごとの分布を考える
下の表より、ウルフとフォックスは平均・分散ともに似ているが、ビールのボトルに関しては平均・分散ともに似ていないことがわかる


ノベルクラスの分布は、ベースクラスに似ているクラスがあれば、それらのクラスの分布で表現できるのではないか?
なぜノベルクラスの「分布」を考えるのか?
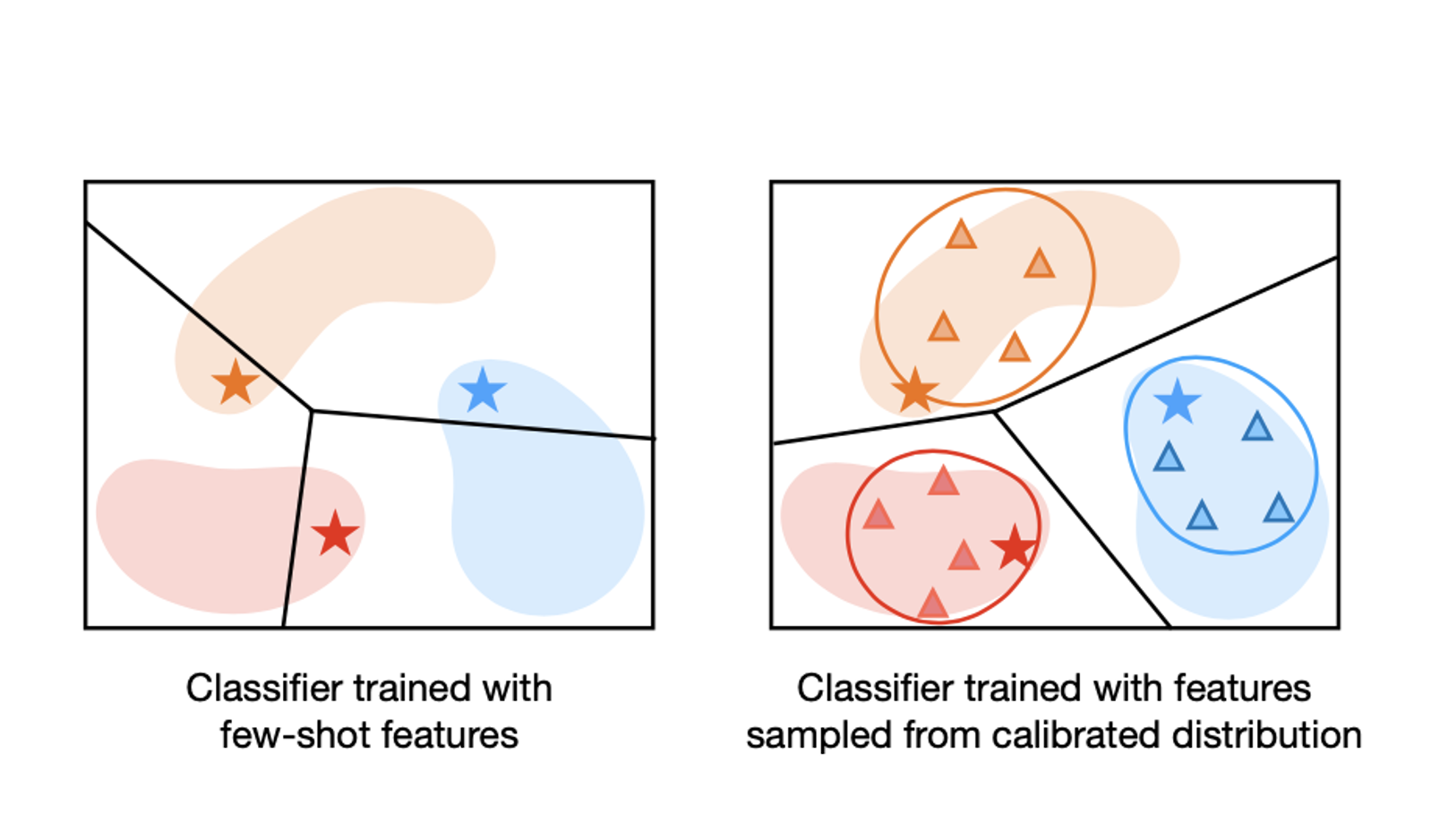
- ノベルクラスの少ないサンプルを使って分類器を学習すると、過剰適合してしまうという問題がある(左図)
- ノベルクラスの分布がわかっていれば、過剰適合することを防ぐことができそう(右図)
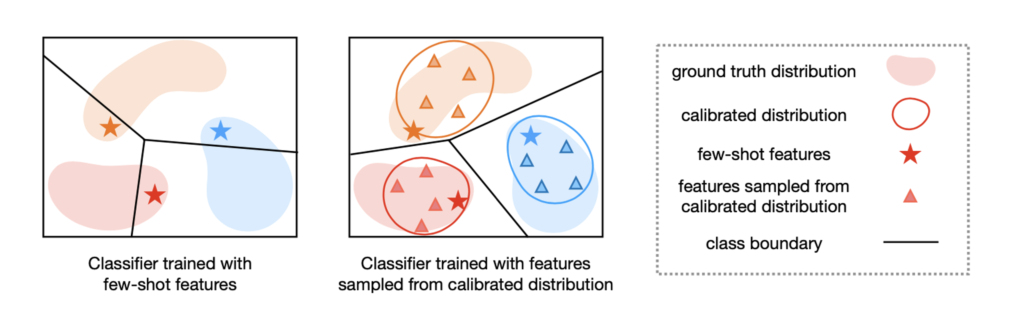
どうやってノベルクラスの分布を推定するのか?
普通に考えてfew-shotしかないノベルクラスの分布を推定することは無理ゲーなので、似ているクラスは特徴空間で分布が似ているという仮説を利用する
まず、ノベルクラスの分布はガウス分布であると仮定
次に、クラスごとにベースクラスの平均と共分散を求める
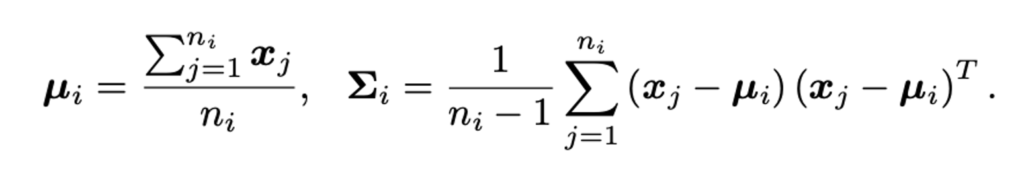
ノベルクラスのデータ(\(\tilde{x}\))とベースクラスの平均の距離をもとに、k番目までの似ているクラスを選ぶ
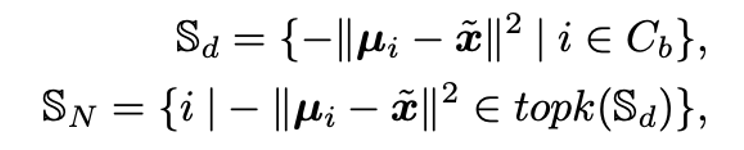
似ているクラスとノベルクラスのデータを平均して、
ノベルクラスの平均と分散を推定する
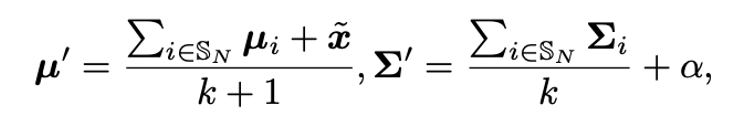
分布からサンプルしたデータを使って学習
ノベルクラスのデータは1つだけでなく、K-shotのときはK個あるので、K個の統計量が得られる(yはNクラスの中のあるクラス)
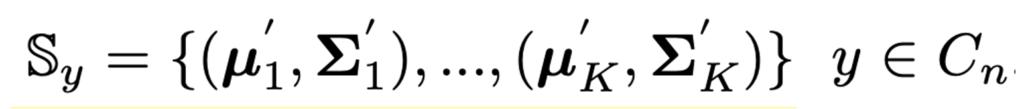
これら全ての統計量から、データをサンプリングする。つまり混合ガウス分布からのサンプリング
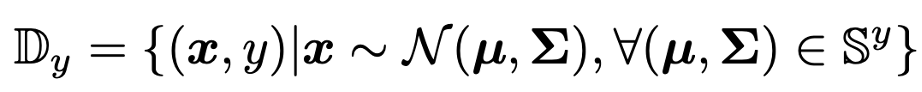
サンプルされたデータと教師yを使って、例えばロジスティック回帰などで学習する(もとのfew-shotのデータ(\(\tilde{S}\))も使う)
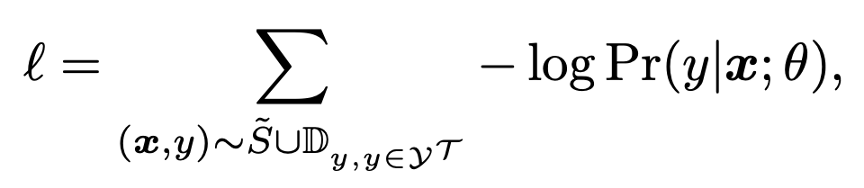
細かいテクニック・ハイパラ
ノベルクラスのデータをガウス分布に従うようにするために、Tukey’s Ladder of Powers Transformation を行う
- λ乗するだけ
- 実験ではλ= 0.5
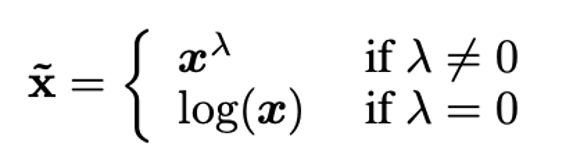
分散度合いをヒューリスティクスに決めている?
- 実験ではα = 0.21 or 0.3
- (αIとか足すことはあるけどαを足すのか…)
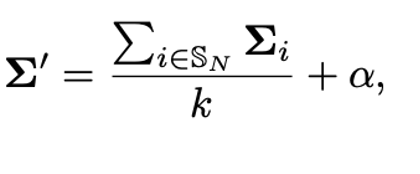
何個のベースクラスの分布を利用するのか(実験では k = 2)
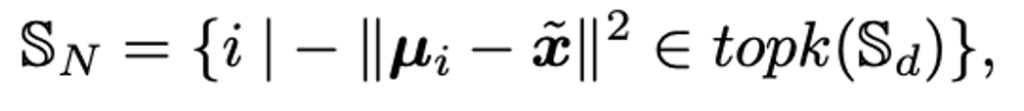
何個くらいサンプルするのか(実験では750くらい)
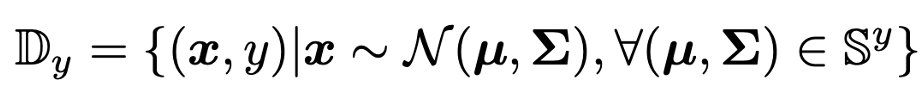
実験
データセット
few-shotでよく使われるのはCUB・miniImageNetというデータセット
この論文では上記に加えてtieredImageNetというデータセットも使って検証している
昔はオムニグロットとか使われてたイメージだが、精度がサチってきて最近では使われなくなってきたイメージ
CUB:
- 200クラスあり、全体で11788サンプル存在し、サイズは84x84x3
- ベースクラス100、検証クラス50、ノベルクラス50
- いろんな鳥が写ってる
miniImageNet:
- 100クラスあり、各クラスごとに600サンプル存在し、サイズは84x84x3
- ベースクラス64、検証クラス16、ノベルクラス20
- ILSVRC-12から取り出された
tieredImageNet:
- 608クラスあり、各クラス平均的に1281サンプル存在する
- ベースクラス351、検証クラス97、ノベルクラス160
- ILSVRC-12から取り出された
評価方法
ノベルクラスからサンプルされる訓練データは5way-1shot or 5way-5shotとする
つまり、訓練データは各クラス1枚か5枚で、5クラス分類をするということ
もちろんベースクラスは無限に使うことができる
上記一回だけだと信頼度がなくなるので、10000回繰り返して平均正解率を求める
テストデータは各訓練データに対し1個?書いてない
実装詳細
- ベースクラス使って学習したWideResNetを特徴抽出器として利用する
- 最終層一層前の特徴を使う
- 活性化関数ReLUの後の特徴を使う
- non-negativeなので、データをλ乗して、ガウシアンっぽくすることが可能
- (ReLUの前を最初から使えばもっとガウシアンっぽくなるのでは?と思ったが、
まあやってるんだろうな)
- 分類器はscikit-learnのLRやSVMを使う
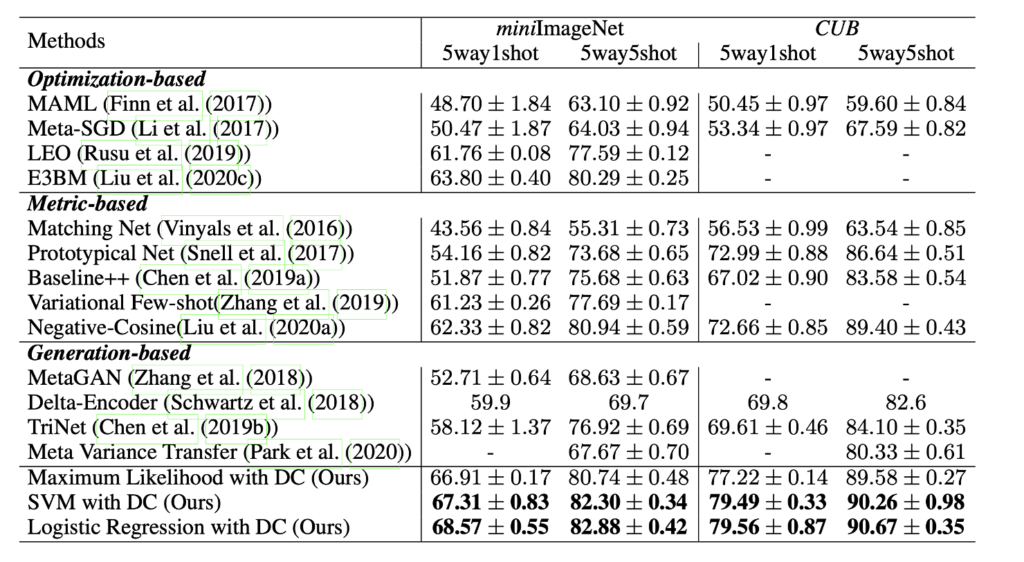
定量的結果
基本的にかなり強い模様
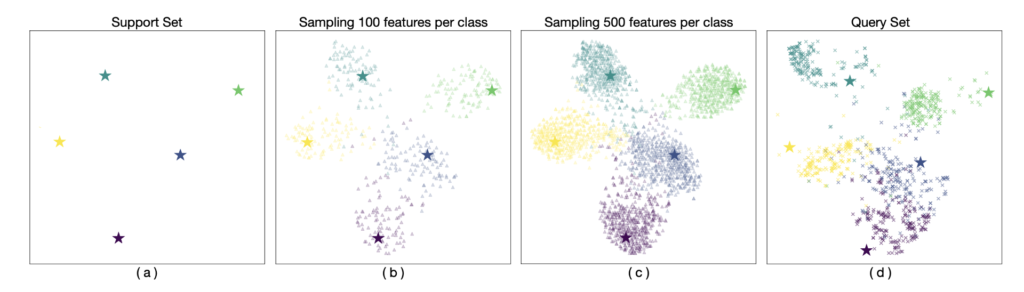
t-SNEを使ってサンプルされたデータを可視化
実際のデータの分布(Query Set)と推定されたデータの分布が似ているので、うまく行っていると言いたいらしい
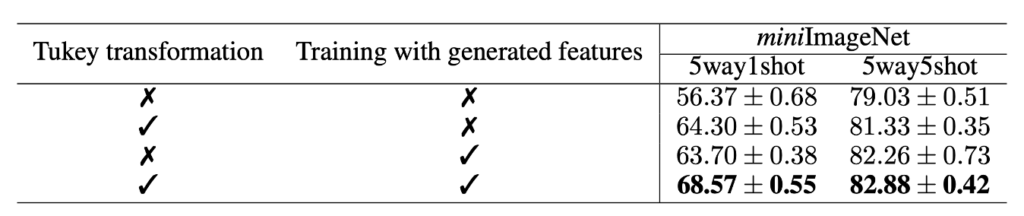
アブレーションスタディ
λ乗するとめちゃくちゃ精度あがるけど、生成サンプル使ってもそこまで精度あがってないようにみえる
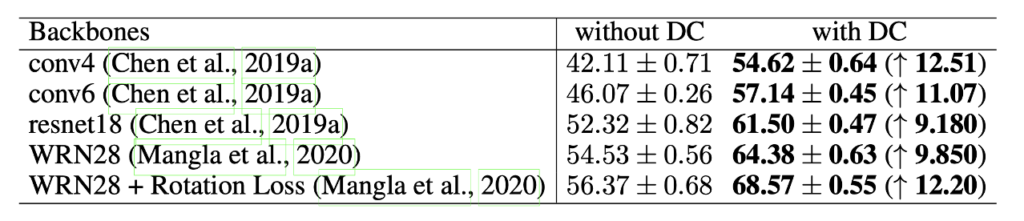
WRN28以外のバックボーン使っても、提案手法によって精度あがることが確認できる
その他実験
ファインチューニングの手法にも適用できる(それはそう)

分布からサンプルされたデータだけを使うより、ノベルクラスから直接得られたサンプルを使うほうが精度よい

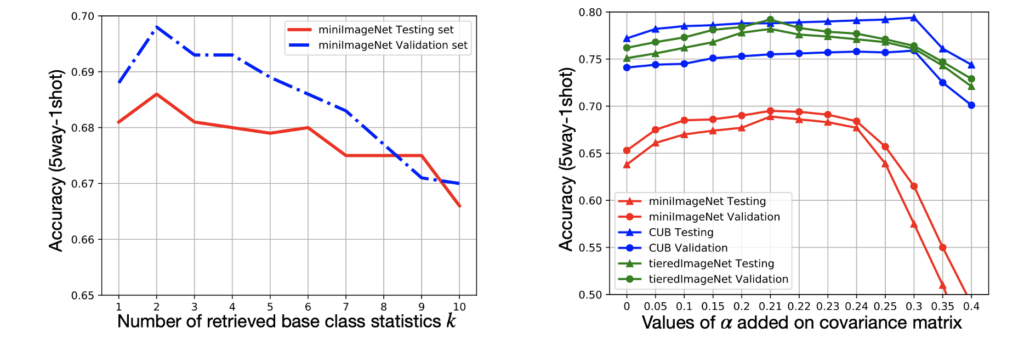
ハイパラ分析
- クラス数はk=2が一番良さそう
- 分散度合いαはデータによる
- バリデーションデータによってハイパラ調整してるっぽい
感想
- 全体としてアイデアは単純で面白いし、結果も出ているようにみえる
- ただ、精度に一番貢献しているのはヒューリスティクス部分なのではないかと思ってる
- Manifold Mixup for Few-shot Learning (WACV 2020)も同じくらい精度でてるけど比較していないのは気になった
- よく読めば理由はわかるかも
- 最後の結論にベースクラスとノベルクラスのドメインが異なった場合はfuture workにするとかいてあり、ベースクラスの分布をもとにノベルクラスの分布が作ることができなくなるので、それはできないのは当然だなという感じがした
- そういった問題設定を解こうとしている論文もいくつかある
- ex) Cross-Domain Few-Shot Classification via Learned Feature-Wise Transformation (ICLR 2020)


コメント