仕事でVATを実装することになったのだが、少なくともMNIST使って精度でないものを使ってもしょうがないということで、まともな実装をいくつか試し、精度がでたものの実装をメモすることにした。
参考にした実装はこちら
実験設定
データセット:MNIST
- training data
- labeled data: 100
- unlabeled data: 49900
- test data: 10000
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
from tqdm import tqdm
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
# load dataset
transform = transforms.Compose([
transforms.ToTensor()
])
dataset = datasets.MNIST('data/mnist', train=True, download=True, transform=transform)
label_unlabel_set, test_set = train_test_split(dataset, random_state=42, test_size=10000)
test_loader = DataLoader(test_set, batch_size=100, shuffle=False)
label_set, unlabel_set = train_test_split(label_unlabel_set, random_state=1, test_size=49900)
label_loader = DataLoader(label_set, batch_size=100, shuffle=True)
unlabel_loader = DataLoader(unlabel_set, batch_size=512, shuffle=True)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# ラベルつきデータの表示
samples, labels = iter(label_loader).next()
argsort = np.argsort(labels)
samples = samples[argsort]
samples = samples.cpu().data.numpy().transpose(0, 2, 3, 1).squeeze()
plt.figure(figsize=(10, 10))
for i in range(100):
plt.subplot(10, 10, i+1)
plt.xticks([])
plt.yticks([])
plt.subplots_adjust(wspace=0., hspace=0.)
plt.imshow(samples[i], cmap=plt.cm.gray)
plt.show()使用したラベルデータは下。きれいにラベルごとに10枚ずつとかはしてない。

モデルは簡単なCNNを使う
class classifier(nn.Module):
def __init__(self):
super(classifier, self).__init__()
self.input_height = 28
self.input_width = 28
self.conv1 = nn.Sequential(
nn.Conv2d(1, 32, kernel_size=4, padding=2),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d(2))
self.conv2 = nn.Sequential(
nn.Conv2d(32, 64, kernel_size=4, padding=2),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(2))
self.fc = nn.Sequential(
nn.Linear((self.input_height // 4) * (self.input_width // 4) * 64, 100),
nn.Dropout(p=0.5),
nn.ReLU(),
nn.Linear(100, 10)
)
initialize_weights(self)
def forward(self, x):
c1 = self.conv1(x)
c2 = self.conv2(c1)
c2_flat = c2.view(c2.size(0), -1)
out = self.fc(c2_flat)
return out
def initialize_weights(model):
for m in model.modules():
if isinstance(m, nn.Conv2d):
m.weight.data.normal_(0, 0.02)
m.bias.data.zero_()
elif isinstance(m, nn.ConvTranspose2d):
m.weight.data.normal_(0, 0.02)
m.bias.data.zero_()
elif isinstance(m, nn.Linear):
m.weight.data.normal_(0, 0.02)
m.bias.data.zero_()
# torch.inference_mode()を使ってみた。早いらしい。
def valid(C, test_loader):
C.eval()
pred, label = [], []
with torch.inference_mode():
for x, y in test_loader:
pred.extend(C(x.to(device)).detach().cpu().numpy())
label.extend(y.numpy())
pred = np.array(pred)
label = np.array(label)
print(confusion_matrix(label, pred.argmax(1)))
print(classification_report(label, pred.argmax(1)))
criterion = nn.CrossEntropyLoss()実験
ラベルあり100枚のみを使うと、どのくらい精度でるのか?
# 100ラベルだけで学習した場合
C = classifier().to(device)
opt = optim.Adam(C.parameters(), lr=0.001)
loss_list = []
for epoch in tqdm(range(500)):
for x, y in label_loader:
pred = C(x.to(device))
loss = criterion(pred, y.to(device))
opt.zero_grad()
loss.backward()
opt.step()
loss_list.append(loss.item())
plt.plot(loss_list)
plt.show()
valid(C, test_loader)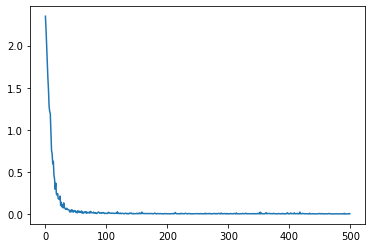
クロスエントロピーロス
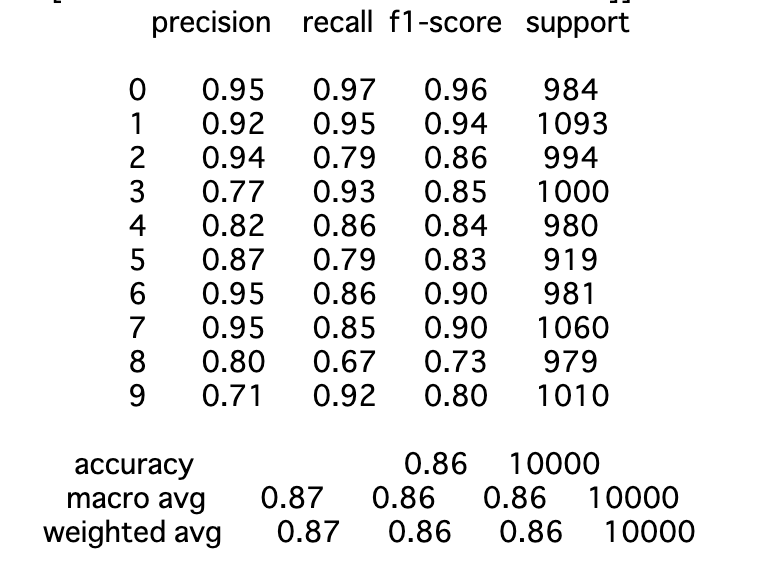
F1 scoreで0.87達成している
100枚だけでもMNISTなのでそこそこ精度がでることがわかった。
ラベルなしデータ49900枚を追加で使うと、どのくらい精度がでるのか?
ここでVATの登場
def kl_div_with_logit(q_logit, p_logit):
q = F.softmax(q_logit, dim=1)
logq = F.log_softmax(q_logit, dim=1)
logp = F.log_softmax(p_logit, dim=1)
qlogq = (q*logq).sum(dim=1).mean(dim=0)
qlogp = (q*logp).sum(dim=1).mean(dim=0)
return qlogq - qlogp
def _l2_normalize(d):
d = d.numpy()
d /= (np.sqrt(np.sum(d ** 2, axis=(1, 2, 3))).reshape((-1, 1, 1, 1)) + 1e-16)
return torch.from_numpy(d)
def vat_loss(model, ul_x, ul_y, xi=1e-6, eps=2.5, num_iters=1):
d = torch.Tensor(ul_x.size()).normal_()
for i in range(num_iters):
d = xi *_l2_normalize(d)
d = d.to(device)
d.requires_grad_()
y_hat = model(ul_x + d)
delta_kl = kl_div_with_logit(ul_y.detach(), y_hat)
delta_kl.backward()
d = d.grad.data.clone().cpu()
model.zero_grad()
d = _l2_normalize(d)
d = d.to(device)
r_adv = eps *d
# compute lds
y_hat = model(ul_x + r_adv.detach())
delta_kl = kl_div_with_logit(ul_y.detach(), y_hat)
return delta_kl「教師なしデータの予測」と「予測ラベルが変わるようなノイズを加えた教師なしデータの予測」を近づける(Local Distributional Smoothing)
LDSも加えて訓練する
C = classifier().to(device)
opt = optim.Adam(C.parameters(), lr=0.001)
ce_loss_list, lds_list = [], []
for epoch in tqdm(range(3000)):
for (x, y), (un_x, _) in zip(label_loader, unlabel_loader):
x = x.to(device)
un_x = un_x.to(device)
pred = C(x)
ce_loss = criterion(pred, y.to(device))
un_y = C(un_x)
lds = vat_loss(C, un_x, un_y)
loss = ce_loss + lds
opt.zero_grad()
loss.backward()
opt.step()
ce_loss_list.append(ce_loss.item())
lds_list.append(lds.item())
plt.plot(ce_loss_list)
plt.show()
plt.plot(lds_list)
plt.show()
valid(C, test_loader)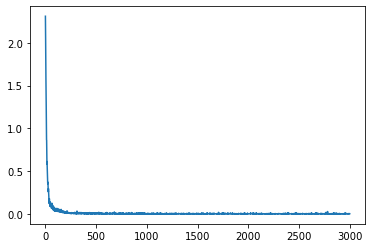
クロスエントロピーロス

LDS
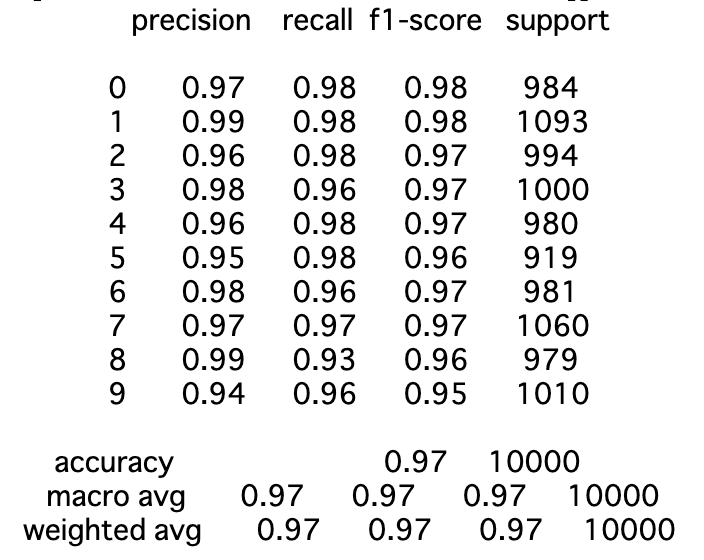
F1 scoreで0.97達成した

パン
簡単な実装で教師なしデータが有効活用できるVATすばらしい…
[追記] 教師なしデータ500枚でもF1値0.95でた。強い。教師なしデータ49900枚もいらなかった説。



コメント