書誌情報
論文タイトル:Very Deep VAEs Generalize Autoregressive Models and Can Outperform Them on Images
論文著者:Rewon Child
この論文を一言でいうと:めっちゃ深い層の階層的なVAEはめっちゃ鮮明な画像を出力できる

訓練方法がVAEと同じなら、モデルのコードさえわかれば完全に理解できるのでは…?
実装参考:https://github.com/openai/vdvae
その他参考文献:
- [Vahdat+ 2020] NVAE: A Deep Hierarchical Variational Autoencoder (NIPS 2020)
- [Klushyn+ 2019] Learning Hierarchical Priors in VAEs (NIPS 2019)
- [Tomczak+ 2017] VAE with a VampPrior
階層的VAEの関連研究
これまで、VAEの潜在変数の分布を標準正規分布に近づけるような「過正則化」を防ぐために、階層化事前分布が提案されている [Klushyn+ 2019][Tomc zak+ 2017]
NVAE [Vahdat+ 2020]では、事前分布と近似事後分布の表現力をあげるために、潜在変数をdisjointなグループに分解($z = {z_1, z_2, …, z_L}$)し、事前分布$p(z)$と近似事後分布$q(z|x)$を次のように表現している
$p(z) = \prod_l^L p(z_l|z_{<l}), q(z|x) = \prod_l^L q(z_l|z_{<l}, x)$
このようにすることで、各潜在変数が相関を持つようなモデル化を行うことができる。このとき、損失関数は以下のようになる
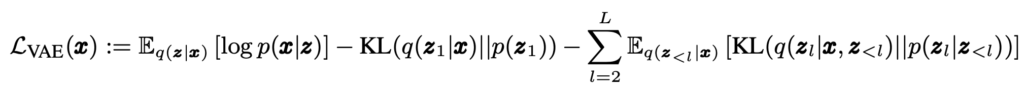
VDVAEでもNVAEと同様の損失関数を使って学習しているようなので、この部分の実装をみていく
VDVAEのモデルの実装
vae.pyにVDVAEの全てが詰まってそうなので、この中身をみていく
全体像
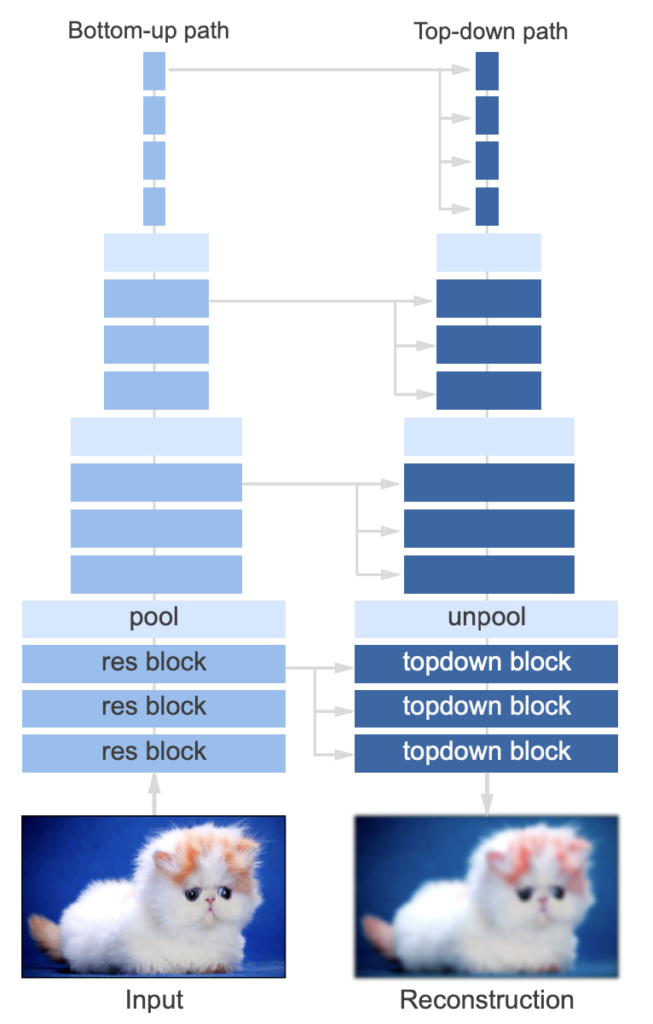

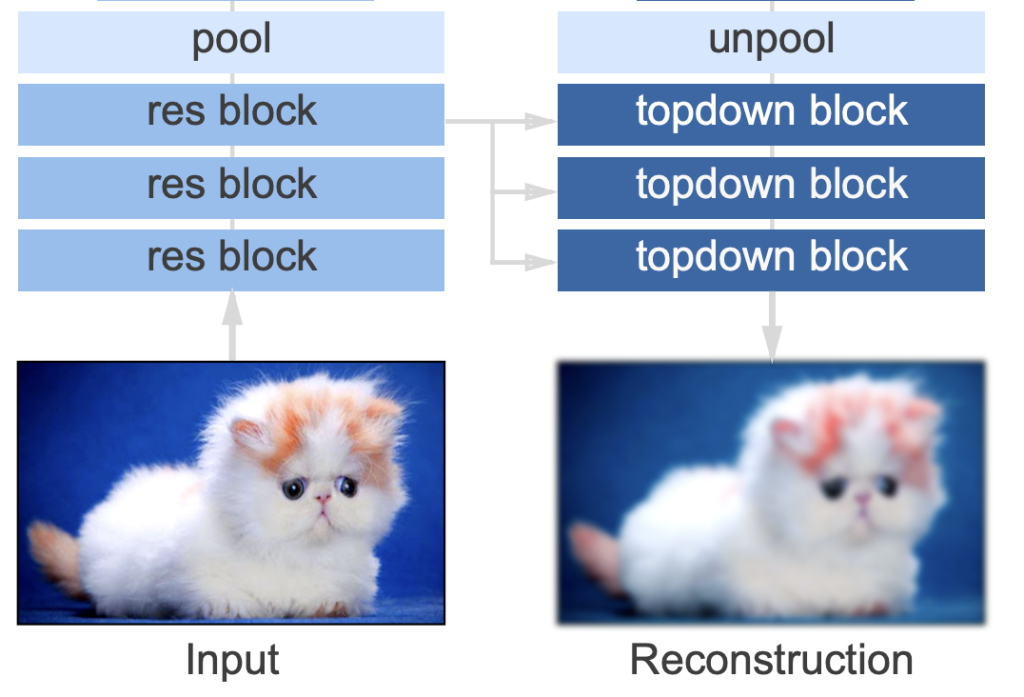
Unetみたいな構造をしてるね。エンコーダの特徴マップのデコーダへの入力の仕方に工夫があるのかな?
主に2つのブロック(res block・topdown block)で構成されているらしい
res block
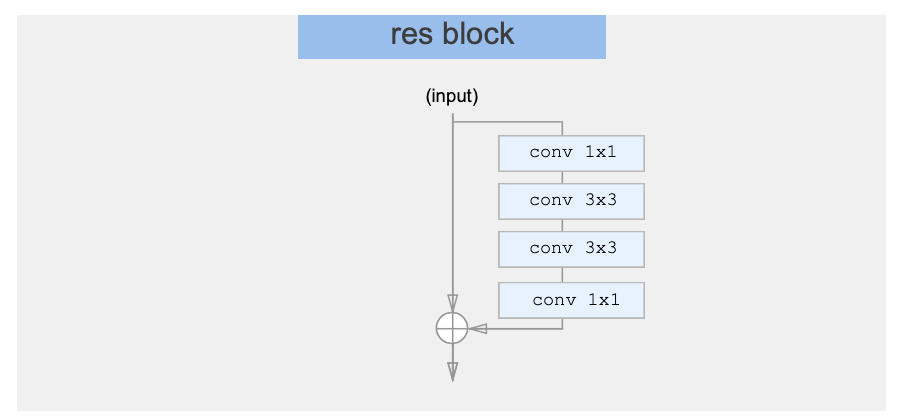

コードのBlockがres blockに対応しているね
class Block(nn.Module):
def __init__(self, in_width, middle_width, out_width, down_rate=None, residual=False, use_3x3=True, zero_last=False):
super().__init__()
self.down_rate = down_rate
self.residual = residual
self.c1 = get_1x1(in_width, middle_width)
self.c2 = get_3x3(middle_width, middle_width) if use_3x3 else get_1x1(middle_width, middle_width)
self.c3 = get_3x3(middle_width, middle_width) if use_3x3 else get_1x1(middle_width, middle_width)
self.c4 = get_1x1(middle_width, out_width, zero_weights=zero_last)
def forward(self, x):
xhat = self.c1(F.gelu(x))
xhat = self.c2(F.gelu(xhat))
xhat = self.c3(F.gelu(xhat))
xhat = self.c4(F.gelu(xhat))
out = x + xhat if self.residual else xhat
if self.down_rate is not None:
out = F.avg_pool2d(out, kernel_size=self.down_rate, stride=self.down_rate)
return outこれは通常のres blockのよう
class Encoder(HModule):
def build(self):
H = self.H
self.in_conv = get_3x3(H.image_channels, H.width)
self.widths = get_width_settings(H.width, H.custom_width_str)
enc_blocks = []
blockstr = parse_layer_string(H.enc_blocks)
for res, down_rate in blockstr:
use_3x3 = res > 2 # Don't use 3x3s for 1x1, 2x2 patches
enc_blocks.append(Block(self.widths[res], int(self.widths[res] * H.bottleneck_multiple), self.widths[res], down_rate=down_rate, residual=True, use_3x3=use_3x3))
n_blocks = len(blockstr)
for b in enc_blocks:
b.c4.weight.data *= np.sqrt(1 / n_blocks)
self.enc_blocks = nn.ModuleList(enc_blocks)
def forward(self, x):
x = x.permute(0, 3, 1, 2).contiguous()
x = self.in_conv(x)
activations = {}
activations[x.shape[2]] = x
for block in self.enc_blocks:
x = block(x)
res = x.shape[2]
x = x if x.shape[1] == self.widths[res] else pad_channels(x, self.widths[res])
activations[res] = x
return activations
Encoderは通常のres blockで構成されてて、中間の特徴マップ(activation)を辞書として保存してるだけみたい
topdown block
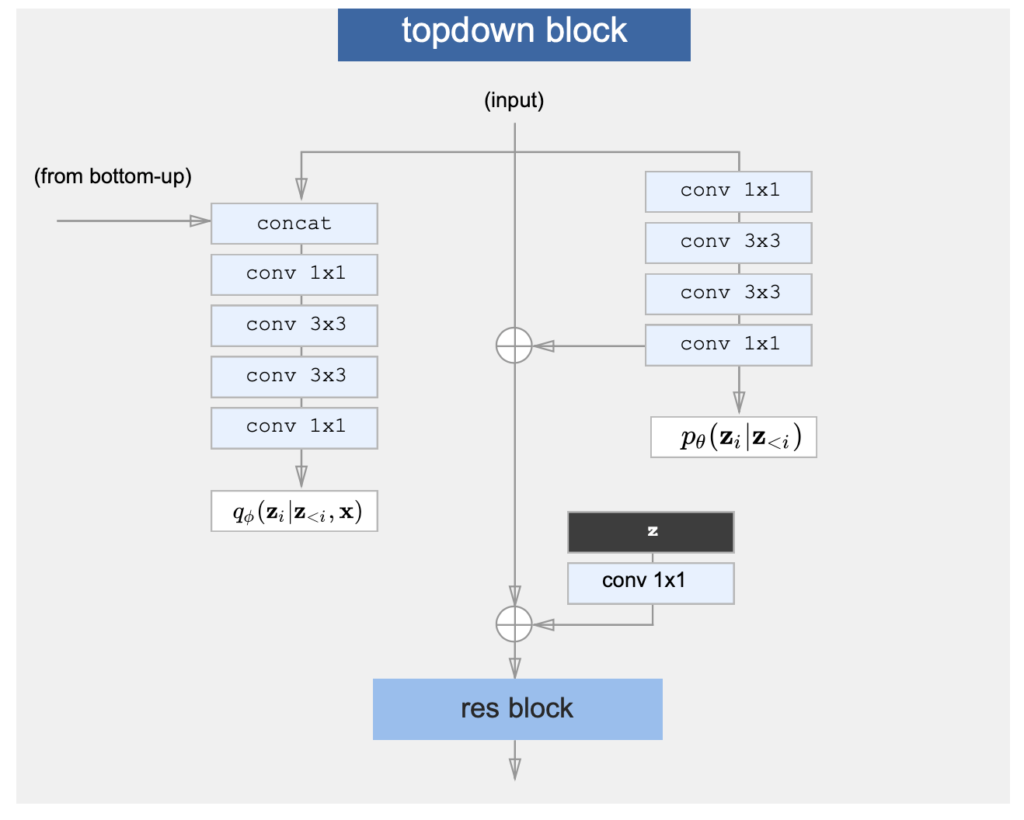

デコーダの要素の一つである、topdown blockは少し複雑だね
コードのDecBlockクラスが対応しているみたいだけど…
class DecBlock(nn.Module):
def __init__(self, H, res, mixin, n_blocks):
super().__init__()
# 中略
def sample(self, x, acts):
qm, qv = self.enc(torch.cat([x, acts], dim=1)).chunk(2, dim=1)
feats = self.prior(x)
pm, pv, xpp = feats[:, :self.zdim, ...], feats[:, self.zdim:self.zdim * 2, ...], feats[:, self.zdim * 2:, ...]
x = x + xpp
z = draw_gaussian_diag_samples(qm, qv)
kl = gaussian_analytical_kl(qm, pm, qv, pv)
return z, x, kl
def forward(self, xs, activations, get_latents=False):
x, acts = self.get_inputs(xs, activations)
if self.mixin is not None:
x = x + F.interpolate(xs[self.mixin][:, :x.shape[1], ...], scale_factor=self.base // self.mixin)
z, x, kl = self.sample(x, acts)
x = x + self.z_fn(z)
x = self.resnet(x)
xs[self.base] = x
if get_latents:
return xs, dict(z=z.detach(), kl=kl)
return xs, dict(kl=kl)
- DecBlockはEncoderからの特徴マップ(activation)と上からの入力(x)をうけとって、それを新しいDecBlockに流す
- 特徴マップと入力をもとに潜在変数をサンプリングし、ついでに損失関数で必要となるKL項も計算する
ということがわかった

モデルの重みも公開されてるので、自分のデータを使ってモデルをファインチューニングできるといいね



コメント